We wanted to see how well does VASP 5.4.4 scales on CPU Nodes at Salomon and Barbora supercomputers at IT4Innovations National supercomputing center in Ostrava, Czech republic.
Those clusters in question are both x86, Intel-based CPU clusters. Though Barbora has 8 nodes with 4x Tesla V100 each, those will not be a subject of this test. Salomon has 24 cores per node in two sockets, Barbora has 36 nodes per node in the same configuration.
For the test case, a 3x2x2 supercell of PtN2 fluorite was used, as this will give us reasonably large calculation to run the tests on as much as 64 nodes. The number of irreducible k-points is 45 and the number of bands is 786. Total of 10 iterations were ran for each of the tests and the average time of one iteration will be used to compare the results (grep LOOP OUTCAR - the "real time" value).
A number of different configurations of KPAR and NCORE parameters were used to see which one behaves the best with this type of calculation. It is however impractical, maybe even impossible, to run multiple tests for each calculation just to determine which configuration will yield the results in the shortest time. To mitigate this issue a "default strategy" will be defined. This rule of thumb is based on the previous experience and it seemed to have produced very good results in these tests as well.
The "default strategy" is following. KPAR=<number-of-CPU-sockets>, which in our case is 2 per each node. NCORE is then equal to the number of cores in each socket. In our case that's 12 on Salomon and 18 on Barbora. Equally, NPAR could be set to 1, but that would fall apart when the KPAR would change, so I find it more convenient to set the NCORE parameter instead. NSIM is equal to 4 as the NSIM parameter has been observed to have produced minimal speedup on non-accelerated nodes. The number of MPI processes per node is equal to the number of cores on that node and OMP_NUM_THEADS is 1.
Let's take a look at the results. The results in tabular form will be attached at the end of this post.
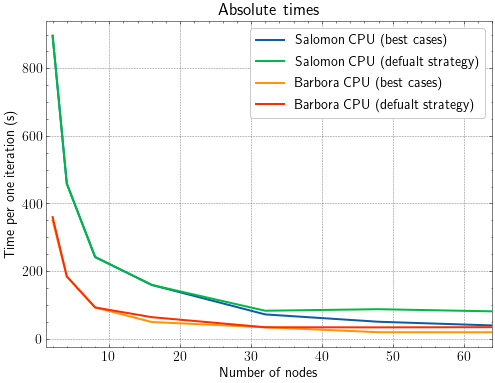
Note, how the default strategy and best cases start to differ at 32 nodes and more. This will be more visible in the following figures.
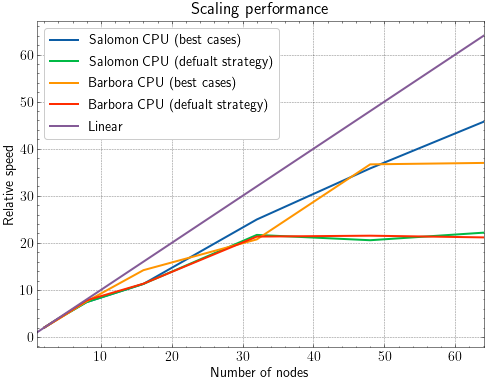
Here, we can see that both on Salomon and on Barbora, the scaling of the default strategy practically stops at above 32 nodes. The comment about the reason will be presented below these figures.
The scaling performance for given number of nodes is calculated relative to the performance of the smallest number of nodes (in this case 2) in given data set.
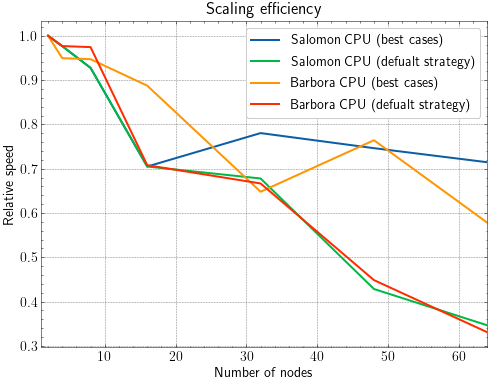
This last figure is another visualization of the scaling. Here, the scaling performance from the second figure is divided by the number of nodes on which the job ran. This gives an efficiency of the scaling relative to the lowest number of nodes (in our case 2). That's the reason why above 32 nodes, the efficiency remains non-zero. Different way to visualize this would be to compare the increase of performance to the increase of the number of nodes. In that case, we would see efficiency around 0 for default strategies above 32 nodes.
The reason why this drop in efficiency happens becomes obvious when looking at the tabular data at the end of this post. The default strategy is trying to push KPAR > 45, even though there is only 45 k-points in the calculation. VASP does not complain about this, but the inefficiency of doing so pretty much zeroes the effect of adding more nodes to the calculation.
However, if one makes a short run of VASP to see how many irreducible k-points there will be, the issue can be easily compensated for and the default strategy when KPAR would need to be larger that the number of k-points will change. On such number of nodes, it would be as following: increase the KPAR is much as possible without saturation of k-points and set NCORE to the number of cores on one node. With this addition the default strategy will get very close to the best cases (as seen in the tabular data e.g. for Salomon, Barbora behaves bit more unpredictably).
Another thing to bear in mind is to spread the load of k-points as equally as possible. This is not an issue when <number-of-k-points>/KPAR is high (let's say above 10). But when it's close to 1 or 2, one must be careful. If KPAR is for example 30 and the number of irreducible k-points is 45, then the first group of 30 k-points is computed in parallel. But the remaining 15 k-points can occupy only half of the cores, leaving the other half waiting. Ideally <number-of-k-points>/KPAR is a whole number, but that can break the default strategy and introduce an unwanted communication overhead.
Last but not least, from the default strategy is evident that as long as the ratio between the number of nodes and KPAR is constant, the memory requirements (per node) will stay more or less constant as well. So if one can fit a calculation into memory on 1 node with KPAR=1, theoretically they should be able to able to fit that into memory also on 32 nodes with KPAR=32. This of course assumes, that there is enough k-points (and it can break the load balancing).
It is also evident, that halving this ratio effectively halves the memory usage. So setting KPAR lower than the default strategy defines is necessary to fit larger jobs into memory.
Tabular results
Salomon CPU (best cases)
| NODES | LOOP REAL | PS CPU | PS MEM | ITERS | KPAR | NCORE | NSIM | KPOINTS | ATOMS | NBANDS |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 896.27 | 98.0042 | 58.1 | 10 | 4 | 12 | 4 | 45 | 192 | 768 |
| 4 | 458.865 | 96.3542 | 59.9 | 10 | 8 | 12 | 4 | 45 | 192 | 768 |
| 8 | 241.563 | 93.0958 | 59.4 | 10 | 16 | 12 | 4 | 45 | 192 | 768 |
| 16 | 158.958 | 86.5625 | 59 | 10 | 32 | 12 | 4 | 45 | 192 | 768 |
| 32 | 71.7904 | 89.4583 | 31.2 | 10 | 32 | 24 | 4 | 45 | 192 | 768 |
| 48 | 50.0431 | 89.2792 | 21.5 | 10 | 32 | 24 | 4 | 45 | 192 | 768 |
| 64 | 39.202 | 82.6958 | 16.8 | 10 | 32 | 24 | 4 | 45 | 192 | 768 |
Salomon CPU (defualt strategy)
| NODES | LOOP REAL | PS CPU | PS MEM | ITERS | KPAR | NCORE | NSIM | KPOINTS | ATOMS | NBANDS |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 896.27 | 98.0042 | 58.1 | 10 | 4 | 12 | 4 | 45 | 192 | 768 |
| 4 | 458.865 | 96.3542 | 59.9 | 10 | 8 | 12 | 4 | 45 | 192 | 768 |
| 8 | 241.563 | 93.0958 | 59.4 | 10 | 16 | 12 | 4 | 45 | 192 | 768 |
| 16 | 158.958 | 86.5625 | 59 | 10 | 32 | 12 | 4 | 45 | 192 | 768 |
| 32 | 82.6463 | 82.6792 | 59.2 | 10 | 64 | 12 | 4 | 45 | 192 | 768 |
| 48 | 87.1981 | 86.8958 | 59.4 | 10 | 96 | 12 | 4 | 45 | 192 | 768 |
| 64 | 80.8726 | 82.5125 | 59.3 | 10 | 128 | 12 | 4 | 45 | 192 | 768 |
Barbora CPU (best cases)
| NODES | LOOP REAL | PS CPU | PS MEM | ITERS | KPAR | NCORE | NSIM | KPOINTS | ATOMS | NBANDS |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 349.713 | 96.1111 | 19.7 | 10 | 2 | 36 | 4 | 45 | 192 | 768 |
| 4 | 184.171 | 95.5028 | 39.6 | 10 | 8 | 18 | 4 | 45 | 192 | 768 |
| 8 | 92.3066 | 86.8194 | 39.6 | 10 | 16 | 18 | 4 | 45 | 192 | 768 |
| 16 | 49.2612 | 92.7528 | 21.6 | 10 | 16 | 18 | 4 | 45 | 192 | 768 |
| 32 | 33.7342 | 96.0639 | 39.6 | 10 | 64 | 18 | 4 | 45 | 192 | 768 |
| 48 | 19.069 | 94.3889 | 21.6 | 10 | 48 | 18 | 4 | 45 | 192 | 768 |
| 64 | 18.9109 | 93.675 | 21.6 | 10 | 64 | 18 | 4 | 45 | 192 | 768 |
Barbora CPU (defualt strategy)
| NODES | LOOP REAL | PS CPU | PS MEM | ITERS | KPAR | NCORE | NSIM | KPOINTS | ATOMS | NBANDS |
|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 359.778 | 97.7361 | 39.6 | 10 | 4 | 18 | 4 | 45 | 192 | 768 |
| 4 | 184.171 | 95.5028 | 39.6 | 10 | 8 | 18 | 4 | 45 | 192 | 768 |
| 8 | 92.3066 | 86.8194 | 39.6 | 10 | 16 | 18 | 4 | 45 | 192 | 768 |
| 16 | 63.5415 | 91.0806 | 39.6 | 10 | 32 | 18 | 4 | 45 | 192 | 768 |
| 32 | 33.7342 | 96.0639 | 39.6 | 10 | 64 | 18 | 4 | 45 | 192 | 768 |
| 48 | 33.4336 | 91.5639 | 39.6 | 10 | 96 | 18 | 4 | 45 | 192 | 768 |
| 64 | 34.0071 | 93.775 | 39.6 | 10 | 128 | 18 | 4 | 45 | 192 | 768 |
LOOP REAL is average time per one iteration in seconds. PS CPU is the average CPU utilization in % from 10 samples at random times. PS MEM is the highest memory usage in % from 10 random samples. ITERS is the number of performed iterations.
Note the constant memory usage in both default strategies. This is because the ratio between number of nodes and KPAR is constant.
